
The p value can be a false positive and to avoid that we can decrease the significance level TYPE I and TYPE II error. So the effect size is an standardized measure of the magnitude of the observed effect 10 ) is that does not tell us the importance of the effect, but we can measure the size of the effect in a standardized way. The problem with the significance (whether is. This is the opposite of the probability that a given test will not find an effect assuming that one exists in the population, which, as we have seen, is the β-level (i.e., Type II error rate” (Field, 2017, p.
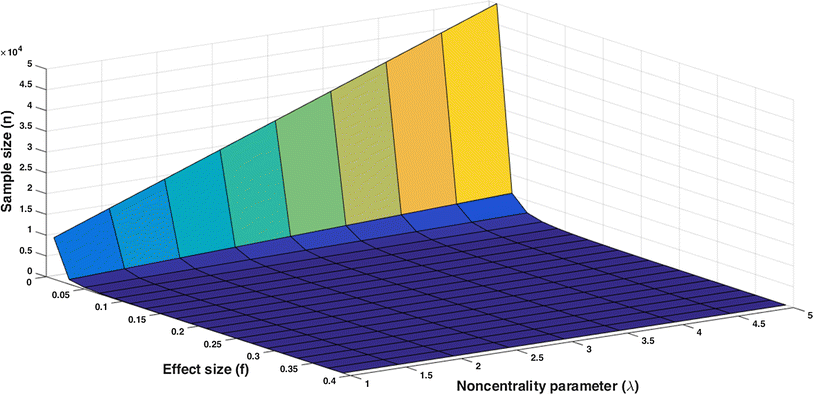
“The power of a test is the probability that a given test will find an effect assuming that one exists in the population. This means that if we took 100 samples (in which the effect exists) we will fail to detect the effect in 20 of those samples. The most common acceptable probability of this error is. The opposite (or false negative) is when we believe that there is no effect where in reality there is. Sample 4 Type I and Type II Errors A Type I error (or false positive) is when we believe that there is a genuine effect when it is not. r = 0.50 (large effect): The effect accounts for 25% of the variance. r = 0.30 (medium effect): The effect accounts for 9% of the total variance. Cohen’s also suggested some common sizes (Field, 2017) r = 0.10 (small effect): In this case the effect explains 1% of the total variance. Pearson’s r “correlation coefficient” that is typically known as the measure of relationships between continuous variables, can also be used to quantify the differences in means between two groups (similar to Cohen’s d). Cohens’ suggestions about what constitutes a large, medium or large effects are: d = 0.2 (small), d = 0.5 (medium) d = 0.8 (large). 2) In general, Cohen's d is defined as where d represents the effect size, μ1 and μ2 represent the two population means, and σ∊ represents the pooled within-group population standard deviation, but in practice we use the sample data means. Similar to other means of standardization such as z scoring, the effect size is expressed in standard score units” (Salkind, 2010, p. “Cohen's d statistic represents the standardized mean differences between groups. This calculation shows an estimated to calculate the size of observed differences between groups: small, medium or large. The Cohen’s effect size is used as a complement to the significance test to show the magnitude of that significance or to represent the extent to which a null hypothesis is false. There are many tools and tables to calculate the effect size. 57) Effect is very important because in addition to our test being significant, we can test "how significant' is the effect.
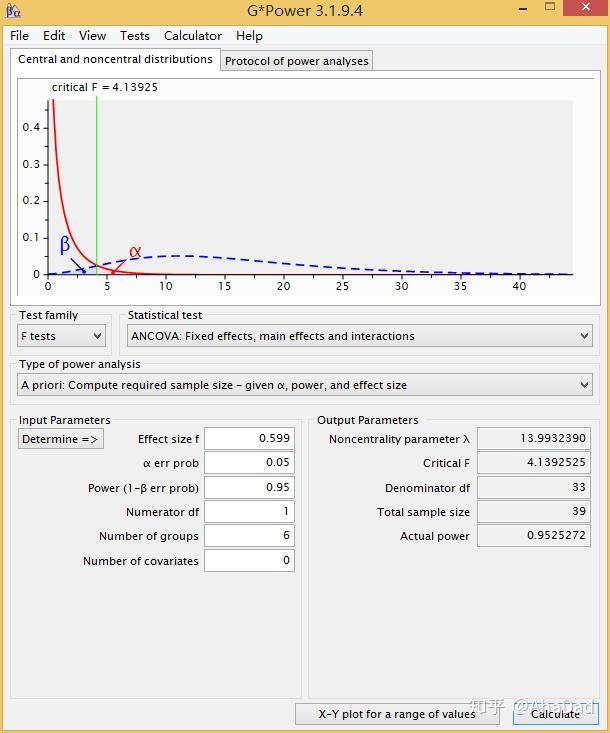
The fact that the measure is standardized just means that we can compare effect sizes across different studies that have measured different variables Many measures of effect size have been proposed, the most common of which are Cohen's d, Pearson's correlation coefficient r and the odds ratio" (Field, 2009, p. About effect size: An effect size is simply an objective and (usually) standardized measure of the magnitude of observed effect. Also, the specific tests to be performed play a role in this calculation (For example factor analysis). The size, the power, and the effect are intimately related. Ouline: General Research Proposal Scenario Cohen’s d effect concept Pearson’s r effect concept Type I and Type II errors Cohen’s d tables Calculating sample size Pearson’s r tables G*Power Tool Linear Regression a priori ANOVA a priori ANOVA post hoc Questions?Ĭommon Scenario on Proposals on URM (Pre QRM) or Statistic Classes: “I am conducting a correlational design and my chosen sample size is 25 subject” (no explanations provided) My typical answer: The sample size is something that we cannot just arbitrarily select, but must calculated based on our type of tests, the expected power, and the expected effect. Females 43% Work on management positions 14% Variable One 22% Variable Two 31% Variable Three 34% Variable Four 39% Variable Five 2 in 5 Additional Descriptive statistics 80% More descriptive statistics 450 Subjects live in the city. 3 in 5 We found some descriptive statistics Variable One 14% Variable Two 22% Variable Three 31% Variable Four 34% Variable Five 39% 275 Subjects live in a rural area. PowerĬalculating Sample Size: Cohen’s Tables and G*Power. Power"- Presentation transcript:ġ Calculating Sample Size: Cohen’s Tables and G. Presentation on theme: "Calculating Sample Size: Cohen’s Tables and G.


 0 kommentar(er)
0 kommentar(er)
